1. Równanie krzywoliniowej trasy kabla.

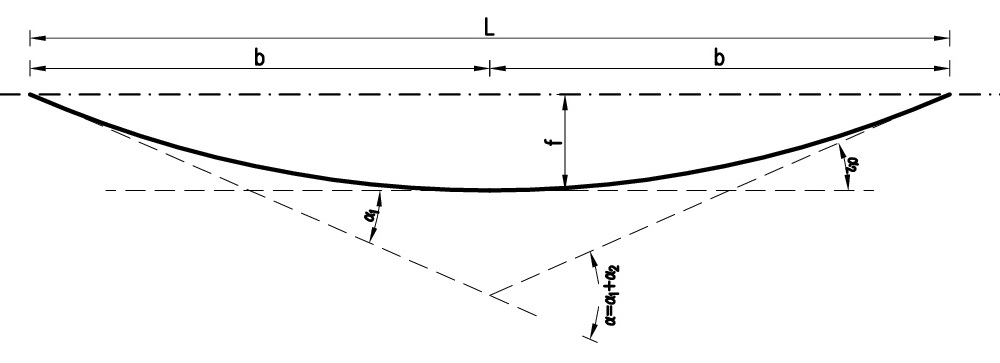
W typowych konstrukcjach trasę kabla sprężającego modeluje się za pomocą odcinków prostoliniowych i krzywoliniowych. Odcinek krzywoliniowy stanowi najczęściej parabola drugiego rzędu o równaniu:

$e(x)=\frac { 4f }{ { L }^{ 2 } } { x }^{ 2 }-\frac { 4f }{ { L } } x$

gdzie:

$f$ – strzałka paraboli

$L$ – długość odcinka paraboli

Obliczając pochodne powyższego równania otrzymujemy:

$e'(x)=\frac { 8f }{ { L }^{ 2 } } { x }-\frac { 4f }{ { L } }$

$e''(x)=\frac { 8f }{ { L }^{ 2 } }$

Przy typowych konstrukcjach belkowych trasa cięgien sprężających jest stosunkowo “płaska” tzn. styczna na ogół nie przecina się z osią pod kątem większym niż $\alpha < 5 deg$ , w związku z tym można przyjąć uproszczenie, że krzywizna trasy parabolicznej jest równa $\kappa \approx |e''(x)|$ , a ponieważ $\kappa = \frac{1}{R}$ otrzymujemy:

$R = \frac{L^2}{8f}$

Zatem trasę paraboliczną możemy w obliczeniach aproksymować łukiem kołowym o promieniu $R$ .

Rozważmy teraz połówkę paraboli opisanej równaniem $e(x)$ i wyznaczmy kąt stycznej na końcu rozważanego odcinka $L$ .

$e'(L)=\frac { 8f }{ { L }^{ 2 } } { L }-\frac { 4f }{ { L } }$

$e'(L)=\frac { 8f }{ L } -\frac { 4f }{ { L } }$

$e'(L)=\frac { 4f }{ L }$

zazwyczaj trasę sprężającą dzielimy na połówki zatem podstawiając $L = 2 \cdot b$

$e'(L)=\frac { 2f }{ b }$

$R = \frac{b^2}{2f}$

2. Wyznaczenie punktu przegięcia na odcinkach przejściowych.

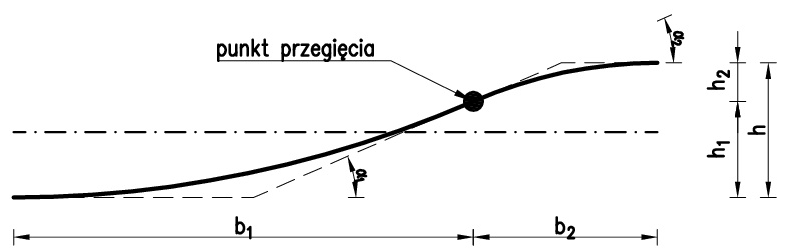
Nad podporami pośrednimi kable przebiegają po trasie parabolicznej o odwrotnej strzałce. Lokalizację punktu przegięcia trasy ustalamy z następujących zależności geometrycznych:

Kąty w punkcie przegięcia obu krzywych wynoszą: $\alpha_1 = \frac{2h_1}{b_1}$ ; $\alpha_2 = \frac{2h_2}{b_2}$ . Z warunku ciągłości w punkcie przegięcia $\alpha_1 = \alpha_2$ . Za pomocą tej zależności oraz danych w postaci: $b_1, b_2, h$ wyznaczamy wysokość $h_1$ oraz $h_2$ :